Summary of Temperature-to-period circuit provides linearization of thermistor response
This article describes a circuit that linearizes the nonlinear response of thermistors by converting temperature into a time period with less than 0.1K error over a 30K range. The design utilizes Bosson's Law to approximate resistance changes, employing a current regulator, buffer amplifier, RC timing network, and comparator to generate oscillation. By adjusting specific resistors, the circuit achieves high sensitivity and stability against supply voltage variations, allowing for digital output via a frequency counter.
Parts used in Thermistor Linearization Circuit:
- Thermistor (RT)
- Parallel Resistance (RP)
- JFET (Q1)
- Resistor RS
- Buffer-Amplifier IC1
- Resistor R4
- Resistor R1
- Capacitor C1
- Resistor R2
- Comparator IC2
- Frequency Counter
Designers often use thermistors rather than other temperature sensors because thermistors offer high sensitivity, compactness, low cost, and small time constants. But most thermistors’ resistance-versus-temperature characteristics are highly nonlinear and need correction for applications that require a linear response. Using a thermistor as a sensor, the simple circuit in Figure 1 provides a time period varying linearly with temperature with a nonlinearity error of less than 0.1K over a range as high as 30K. You can use a frequency counter to convert the period into a digital output. An approximation derived from Bosson’s Law for thermistor resistance, RT, as a function of temperature, θ, comprises RT=AB–θ (see sidebar “Exploring Bosson’s Law and its equation”). This relationship closely represents an actual thermistor’s behavior over a narrow temperature range.
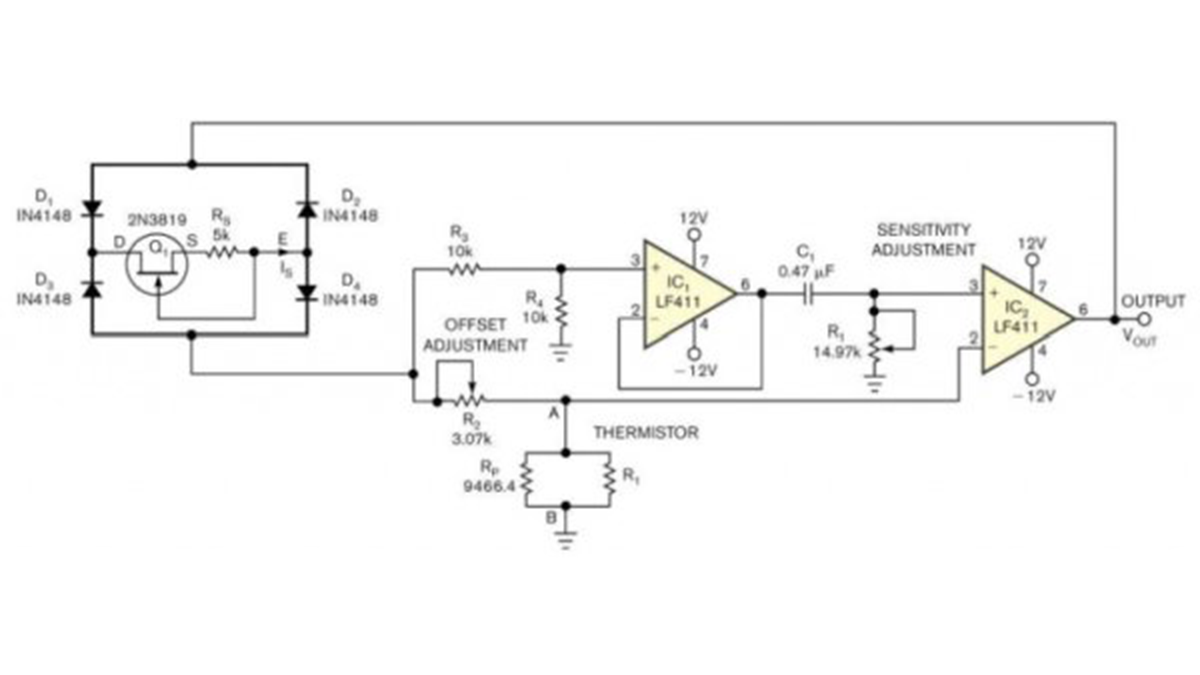
You can connect a parallel resistance, RP, of appropriate value across the thermistor and obtain an effective resistance that tracks fairly close to AB–θ 30K. In Figure 1, the network connected between terminals A and B provides an effective resistance of RAB AB–θ. JFET Q1 and resistance RS form a current regulator that supplies a constant current sink, IS, between terminals D and E.
Through buffer-amplifier IC1, the voltage across R4 excites the RC circuit comprising R1 and C1 in series, producing an exponentially decaying voltage across R1 when R2 is greater than RAB. At the instant when the decaying voltage across R1 falls below the voltage across thermistor RT, the output of comparator IC2 changes its state. The circuit oscillates, producing the voltage waveforms in Figure 2 at IC2‘s output. The period of oscillation, T, is T=2R1C1ln(R2/RAB)2R1C1[ln(R2/A)+θlnB]. This equation indicates that T varies linearly with thermistor temperature θ.
You can easily vary the conversion sensitivity, ΔT/Δθ, by varying resistor R1‘s value. The current source comprising Q1 and R1 renders the output period, T, largely insensitive to variations in supply voltage and output load. You can vary the period, T, without affecting conversion sensitivity by varying R2. For a given temperature range, θL to θH, and conversion sensitivity, SC, you can design the circuit as follows: Let θC represent the center temperature of the range. Measure the thermistor’s resistance at temperatures θL, θC, and θH. Using the three resistance values RL, RC, and RH, determine RP, for which RAB at θC represents the geometric mean of RAB at θL and θH. For this value of RP, you get RAB exactly equal to AB–θ at the three temperatures, θL, θC, and θH.
Read more: Temperature-to-period circuit provides linearization of thermistor response
-
Why do designers often choose thermistors over other temperature sensors?
Designers use thermistors because they offer high sensitivity, compactness, low cost, and small time constants. -
How does the described circuit handle the nonlinearity of thermistors?
The circuit provides a time period varying linearly with temperature with a nonlinearity error of less than 0.1K over a range as high as 30K. -
What law is used to approximate the thermistor resistance behavior?
Bosson's Law is used, comprising the relationship RT=AB–θ which closely represents actual thermistor behavior over a narrow temperature range. -
How can you make the effective resistance track AB–θ over 30K?
You can connect a parallel resistance RP of appropriate value across the thermistor to obtain an effective resistance that tracks fairly close to AB–θ. -
Which components form the current regulator in this circuit?
JFET Q1 and resistance RS form a current regulator that supplies a constant current sink IS between terminals D and E. -
How is the conversion sensitivity varied in the circuit?
You can easily vary the conversion sensitivity ΔT/Δθ by varying resistor R1's value. -
Can the period T be varied without affecting conversion sensitivity?
Yes, you can vary the period T without affecting conversion sensitivity by varying R2. -
How do you determine the value of RP during circuit design?
You determine RP so that RAB at the center temperature θC represents the geometric mean of RAB at the lower limit θL and upper limit θH. -
How is the analog signal converted to a digital output?
You can use a frequency counter to convert the period into a digital output.
