Have you been using float or double variables to perform mathematical operations on embedded systems without a Floating-Point Unit (FPU)? You are doing it wrong! That’s incredibly inefficient. Use fixed-point representation instead.
An FPU is an hardware block specially designed to carry on arithmetic operations on floating point numbers. Even though the C/C++ code may work without an FPU, it’s always much faster to use hardware designed for a specific purpose, like this one, instead of relying on a software implementation, something that the compiler will do for you, knowing the hardware restrictions you have but not in an efficient manner. Essentially, it will generate a lot of assembly code, greatly increasing the size of your program and the amount of time required to complete the operation. Thus, if you don’t have an FPU available and you still want to perform those arithmetic operations efficiently you’ll have to convert those numbers to fixed-point representation. Integers! But how? By scaling them. Let’s see how that scaling value may be determined.
The scaling value as well as the resulting scaled number, which is an integer, really much depends on the bitness of the CPU’s architecture being used. You want to use values that fit in the available registers which have the same width as the CPU buses. So, whether you are working with an 8, 16 or 32-bit architecture, the range of integer values we can store on those registers, being b the number of bits and representing numbers in two’s complement, is given by:
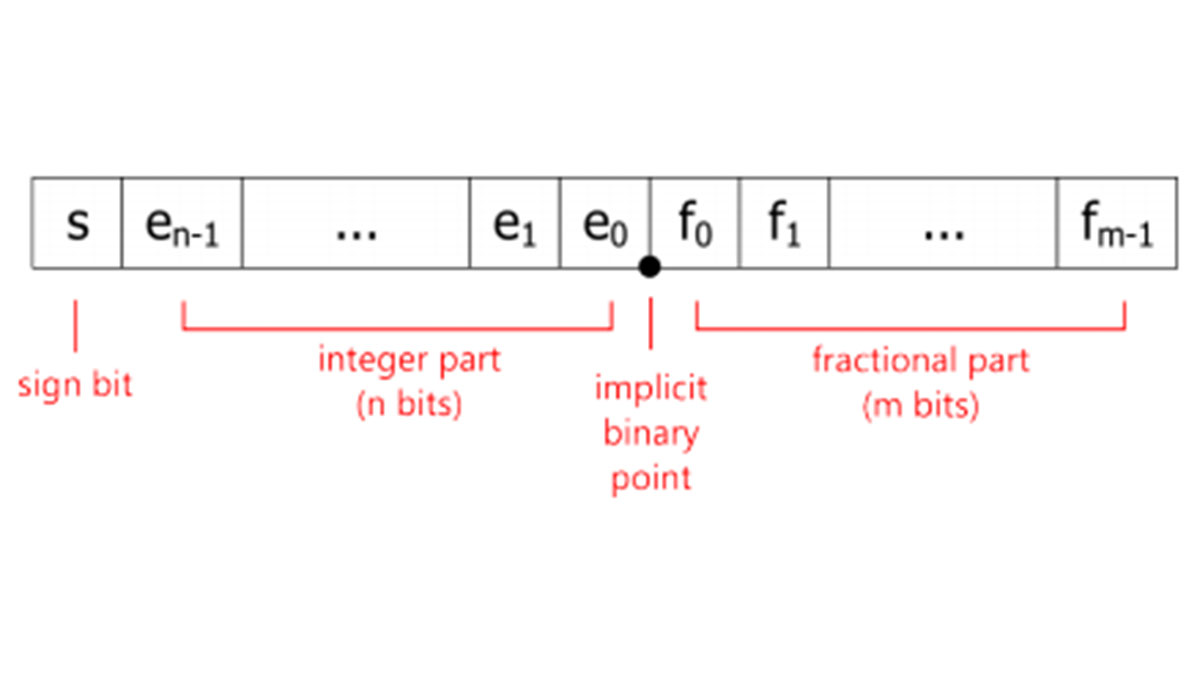
If one bit is used to represent the sign (and in this text we’ll always consider signed numbers) the remaining ones may be used to represent the integer and fractional parts of the floating-point number.We may textually represent this format as follows (denoted as Q-format)
For More Details: The Art of Representing Floating-Point Numbers as Integers
