If you have a load with a variable or poorly specified resistance and want to regulate the power applied to it (a heater for example), merely controlling the voltage or current will not work, as in both cases the power P = I2R = V2/R depends on R.
Instead, let us generate pulses with constant energy Epulse, independent of the resistance of the load RL. Then by changing the frequency f of the pulses we can conveniently and precisely control the load power (P = f·Epulse), from 0 to a known maximum level.
Figure 1a shows a simple way to generate a constant energy pulse. Capacitor C is charged to an initial voltage V0, storing ½CV02 joules. It is then discharged through the load. The pulse has a constant energy that does not depend on RL.
Such a simple approach has drawbacks. First, it is wasteful. In order to charge the capacitor with ½CV02 joules, another ½CV02 joules are lost (see Appendix for details). The circuit of Figure 1b fixes that problem – all resistive losses now occur in the load.
One thing to note is that the power distribution of the pulse is quite uneven. About 63.2% of the energy is delivered in the first ½τ (τ = RLC; energy lost in the load evolves twice as fast as the voltage rises, hence the factor ½). It takes a further ½·4τ for the next 36.1% of energy, which is equivalent to only about 1/7 of the average power during the first ½τ. The uneven power distribution limits the maximum power that can be controlled by the circuit. It takes infinity to transfer the remaining 0.67% of the energy. In practice this will be ignored, limiting accuracy.
However, as shown in Figure 1c, we can interrupt charging after the capacitor has reached a certain threshold value, VC. The energy dissipated in the load is equal to CVCV0 – ½CVC2 and is again independent of the value of RL (see Appendix for derivation).
When choosing the value of VC, the main consideration is overshoot, which causes the energy of the pulse to be higher than calculated. The slew rate at the moment the threshold is reached is equal to:
A lower threshold value VC results in higher overshoot for the same comparator speed.
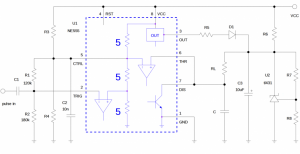
The Design Idea in Figure 2 shows one possible implementation. A 555 provides switches, a comparator, and logic. The trigger input is biased above the trip point by divider R1 & R2. Triggering pulses pass through a small capacitor, C1 (2-10 pF), in order to prevent saturation of the comparator (see 8.3.1 of the datasheet). The maximum operating frequency is therefore comparable to that of an oscillator.
Read more: Circuit delivers constant power to a load